Schriftlich addieren und substrahieren werden in der Regel in der zweiten/dritten Klasse erklärt und geübt. Das Kopfrechnen führt schnell an die Grenzen beim addieren größerer Zahlen. Die Plus-Aufgaben dieser Zahlen können über das schriftliches Prozedere errechnet werden. Dazu wird das addieren und substrahieren in Zahlenraum 10 benötigt.
Einerstelle, Zehnerstelle, Hunderterstelle
Das Ergebnis wird schrittweise errechnet. Die Schritte werden nach der Stelle von der Zahl nach einander ausgeführt. Angefangen wird bei der Einerstelle. Die Einerstelle (E) ist immer die letzte Stelle in der Zahl. Ist die Zahl 15, ist die Einerstelle die 5. Ist die Zahl 5264, ist die Einerstelle die Zahl 4. Die Zehnerstelle (Z) ist immer die zweit letzte Stelle der Zahl. Ist die Zahl 15, ist die Zehnerstelle die 1. Ist die Zahl 5264, ist die Zehnerstelle die Zahl 6. Für die rest der Stellen gilt: Die dritt letzte Stelle ist die Hunderterstelle (H) und die viert letzte Stelle die Tausenderstelle (T) .
Beispiele:
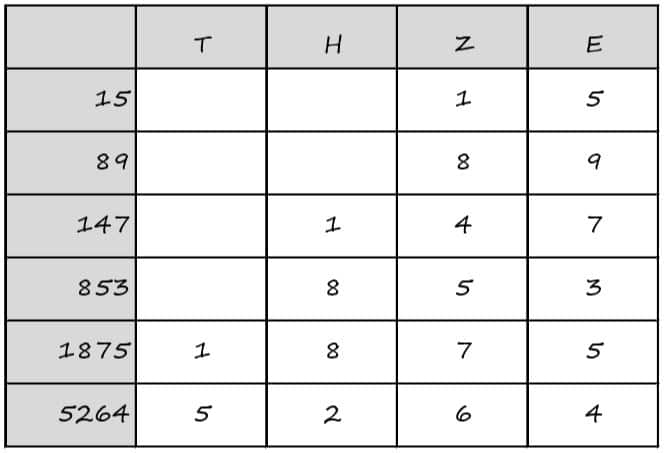
Für das schriftliches Rechnen werden die Zahlen stellengerecht untereinander geschrieben.

Rechenzeichen hinzufügen
Nachdem die Zahlen stellengerecht untereinander geschrieben worden sind, wird das Rechenzeichen Plus oder Minus hinzugefügt. Das Zeichen wird immer links neben der untersten Zahl plaziert.
Plus

Minus
Mit den ersten zwei Schritte wird die Aufgabe übersichtlich dargestellt.
Rechenaufgabe 1: 147+853=
Rechenaufgabe 2: 853-147=
Darstellung:

Mit dem Strich unterhalb der untersten Zahl wird das Ergebnis deutlich von der Aufgabe abgegrenzt.
Die Berechnung
Die Berechnung findet sowohl bei der Addition als auch bei der Substration immer von rechts, von der Einerstelle an.
Rechenaufgabe 1: 232+144=
Rechenaufgabe 2: 468-147=

Unter dem Strich wird das Ergebnis von der Zahl rechtsoben in Zusammenhang mit dem Rechenzeichen und die Zahl rechtsunten notiert. Im Beispiel 2 + 4 = 6 und 8 – 7 = 1.

Rechnen mit Übertrag
In diesen zwei Beispiele wurde die Aufgabe der Einer ohne Zehnerübergang gestellt. Findet jedoch bei der Einer-Aufgabe ein Zehnerübergang statt, reicht es nicht sich nur auf die Einerstelle zu konzentrieren. In diesem Fall wird das Ergebnis mit Übertrag berechnet.

Im ersten Beispiel wird berechnet 8 +4 = 12. Die Zahl 12 wird jetzt wieder in Einer und Zehner unterteilt. In der “Kolom Einer” wird die 2 notiert. Die Zehnerzahl kann nicht in der Einerkolom notiert werden und wandelt als Zahl 1 in der Zehnerkolom, diese Zahl wird bei der nächsten Berechnung von den Zehnerzahlen berücksichtigt.
Im zweiten Bespiel kann die Zahl 7 nicht von der Zahl 5 substrahiert werden. Hier müssen die Zehnerzahlen ein Zehner an die Einerzahl abgeben. Somit wird berechnet 15 – 7 = 8. Damit nicht bei der Zehnerberechnung nicht vergessen wird, dass ein Zehner abgegeben wurde, wird bei den Zehner die Zahl 1 notiert. Diese wird dann bei der Berechnung berücksichtigt.
Sind die Einer berechnet, wird im nächsten Schritt die Zehner berechnet.

Im ersten Beispiel wird berechnet 3 +4 +1 = 18. Im zweiten Beispiel 6 – 4 – 1 = 1.
Für die Berechnung der Hunderter:
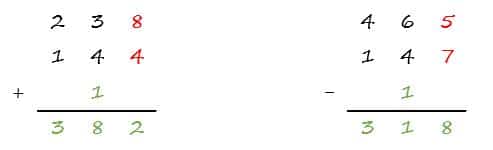
Aufgabe 2: 2683 + 1447
Aufgabe 3: 465 – 147
Aufgabe 4: 4251 – 1473

Aufgabe 3: (E) 15 – 7 = 8, (Z) 6 – 4 – 1 = 1, (H) 4 – 1 = 3
Aufgabe 4: (E) 11 – 3 = 8, (Z) 15 – 7 – 1 = 7, (H) 12 – 4 – 1 = 7, (T) 4 + 1 + 1 = 2
Fazit
Schwierige Plus- und Minusaufgaben können mit dem schriftlichen Verfahren einfach berechnet werden. Voraussetzung ist allerdings, dass das Kopfrechnen im Zahlenraum 10 mit Zehnerübergang gut beherrscht wird.
Übung macht den Meister: Hier geht es zum Übungsmaterial schriftliches Rechnen
Die PDF-Übungsblätter zum schriftlichen Addieren und Substrahieren können Sie kostenlos ausdrucken. Sie brauchen sich dafür nicht anzumelden.
